哈希表
哈希表
242. 有效的字母异位词
给定两个字符串 *s* 和 *t* ,编写一个函数来判断 *t* 是否是 *s* 的字母异位词。
**注意:**若 *s* 和 *t* 中每个字符出现的次数都相同,则称 *s* 和 *t* 互为字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
提示:
1 <= s.length, t.length <= 5 * 104s和t仅包含小写字母
思路分析
第一种方法
首先俩个字符串中的字符出现次数若是一样,具备以下特点:
- 长度相等
- 排序后,俩个字符串相等
我们可以利用这个原理,先将俩个字符串排序,然后比较是否相等
第二种方法
利用hash表,记录s串中每个字符出现的次数,遍历t串中将 hash 表中的对应字符的次数递减。
若hash表中每个字符的出现次数都为0,就说明 s 和 t 是 有效的字母异位词
代码实现
第一种方法
public static boolean isAnagram(String s, String t) {
// 如果俩个字符串长度不相等,直接返回false
if (s.length() != t.length()) return false;
/**
* 对s、t分别排序
* 如果字母出现次数都一样的话,排序后肯定是相等的
* */
String s1 = new String( Arrays.sort(s.toCharArray()));
String s2 = new String(Arrays.sort(t.toCharArray()));
return s1.equals(s2);
}
第二种方法
public static boolean isAnagram1(String s, String t) {
if (s.length() != t.length()) return false;
// 保存字符出现的次数
int[] res = new int[26];
for (int i = 0; i < s.length(); i++) {
/*
* 这里为什么要减 'a' ?
* a~z的ASCII为 97~122,减去'a' 正好得该字符在数组中的位置
* */
// s串中出现字符的次数累加
res[s.charAt(i) - 'a']++;
// t串中出现字符的次数递减
res[t.charAt(i) - 'a']--;
}
// 判断res数组中的值是否全为0,全为0说明s和t字符出现次数相同
for (int val : res) {
if (val != 0) return false;
}
return true;
}
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i]仅包含小写字母
思路分析
异位词的特点:
- 字母相同,但是顺序可能不同
- 长度小相同
那么我们将 异位词 进行排序之后,那么所有的异位词都是相同的。可以利用这个特点,排序过后的 异位词 作为 hash表的key,若key相同则放入同一个集合内!
public List<List<String>> groupAnagrams(String[] strs) {
HashMap<String, List<String>> map = new HashMap<>();
for (int i = 0; i < strs.length; i++) {
// 对每一个单词进行排序
char[] chars = strs[i].toCharArray();
Arrays.sort(chars);
// 排完序之后,异位词变为相同的单词, 放入map集合
List<String> list = map.getOrDefault(String.valueOf(chars), new ArrayList<String>());
list.add(strs[i]);
map.put(String.valueOf(chars),list);
}
// 保存map中分好组的集合
ArrayList<List<String>> res = new ArrayList<>();
map.forEach((key,value) ->{
res.add(value);
});
return res;
}
349. 两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的
提示:
1 <= nums1.length, nums2.length <= 10000 <= nums1[i], nums2[i] <= 1000
思路分析
利用 set 集合不重复的特点,将 nums1、nums2都放入set集合中,然后求交集
代码实现
public static int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set1 = new HashSet<>();
for (int i : nums1) {
set1.add(i);
}
Set<Integer> set2 = new HashSet<>();
for (int i : nums2) {
set2.add(i);
}
// 求交集
set1.retainAll(set2);
// 将交集转换回数组
Integer[] intersection = set1.toArray(new Integer[0]);
// 将 Integer数组转换成 int 数组
return Arrays.stream(intersection).mapToInt(Integer::intValue).toArray();
}
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
思路分析
该题最主要的目的其实就是找和,对于一个数如果他不是快乐数,那么不断的累加平方和,最后肯定会得到一个相等的数,也就是会陷入循环当中。
例如:37
32 + 7 2 = 58
52 + 8 2 = 89
........
22 + 9 2 = 85
82 + 5 2 = 89
........
此时已经出现相同的数了,在求下去就没有必要了。
那么我们的目的,就是要判断 这个和是否出现过,因此我们可以利用 set 集合。
将每次求得平方和加入到这个 set 集合中,然后判断是否出现过,出现过则不是快乐数,没有出现过就知道求到 1 为止。
代码实现
public static boolean isHappy(int n) {
Set<Integer> set = new HashSet<Integer>();
while(n != 1 && !set.contains(n)) {
// 如果n不等于1,并且不包含n,说明这个数还没有求过
set.add(n);
n = getNextNum(n);
}
return n == 1;
}
// 获取下一个求和的数
public static int getNextNum(int n) {
int sum = 0;
while (n != 0) {
// 对n的每个位置上的数进行求和
int digit = n % 10;
sum = sum + digit * digit;
n /= 10;
}
return sum;
}
刚开始想的是用递归,也可以实现此算法,不过LeetCode用不了,很遗憾~~
static Set<Integer> set = new HashSet<Integer>();
public static boolean isHappy1(int n) {
int sum = 0;
while (n != 0) {
//
int digit = n % 10;
sum = sum + digit * digit;
n /= 10;
}
if (sum == 1) return true;
if (set.contains(sum)) return false;
set.add(sum);
// 进行递归
return isHappy(sum);
}
263. 丑数
丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ,请你判断 n 是否为 丑数 。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:n = 6
输出:true
解释:6 = 2 × 3
示例 2:
输入:n = 1
输出:true
解释:1 没有质因数,因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。
示例 3:
输入:n = 14
输出:false
解释:14 不是丑数,因为它包含了另外一个质因数 7 。
提示:
-231 <= n <= 231 - 1
思路分析
简单来说将一个数的因数分解到不能再分解后,如果包含2、3、5就说明这个数是丑数!
若是丑数,换成公式则为:n = 2a + 3b +5c
为判断 n 是否满足上述形式,可以对 n 反复除以 2,3,5,直到 n 不再包含质因数 2,3,5。若剩下的数等于 1,则说明 n 不包含其他质因数,是丑数;否则,说明 n 包含其他质因数,不是丑数。
public boolean isUgly(int n) {
if (n < 1) return false;
while (n % 2 == 0) {
n /= 2;
}
while (n % 3 == 0) {
n /= 3;
}
while (n % 5 == 0) {
n /= 5;
}
return n == 1;
}
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
思路分析
最容易想到的无疑是暴力法,直接双层for循环,挨个去加。
// 暴力法
public static int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
for (int i = 0; i < nums.length; i++) {
for (int j = i+1; j < nums.length; j++) {
int sum = nums[i] + nums[j];
if (sum == target) {
res[0] = i;
res[1] = j;
break;
}
}
}
return res;
}
第二种方法:hash表
使用hash表,可以考虑使用什么样的hash表? set ? map?
题目中要求返回下标,并且我们还需要知道下标和值的对应关系,因此选用map。那么接下来考虑怎么存储?
我们要根据某个值来返回对应的下标,因此存储关系为:
当我们遍历数组时,只需要在 hash表中查找是否有与当前值匹配的值即可,若没有将当前值放入hash表,如果有直接返回下标即可。
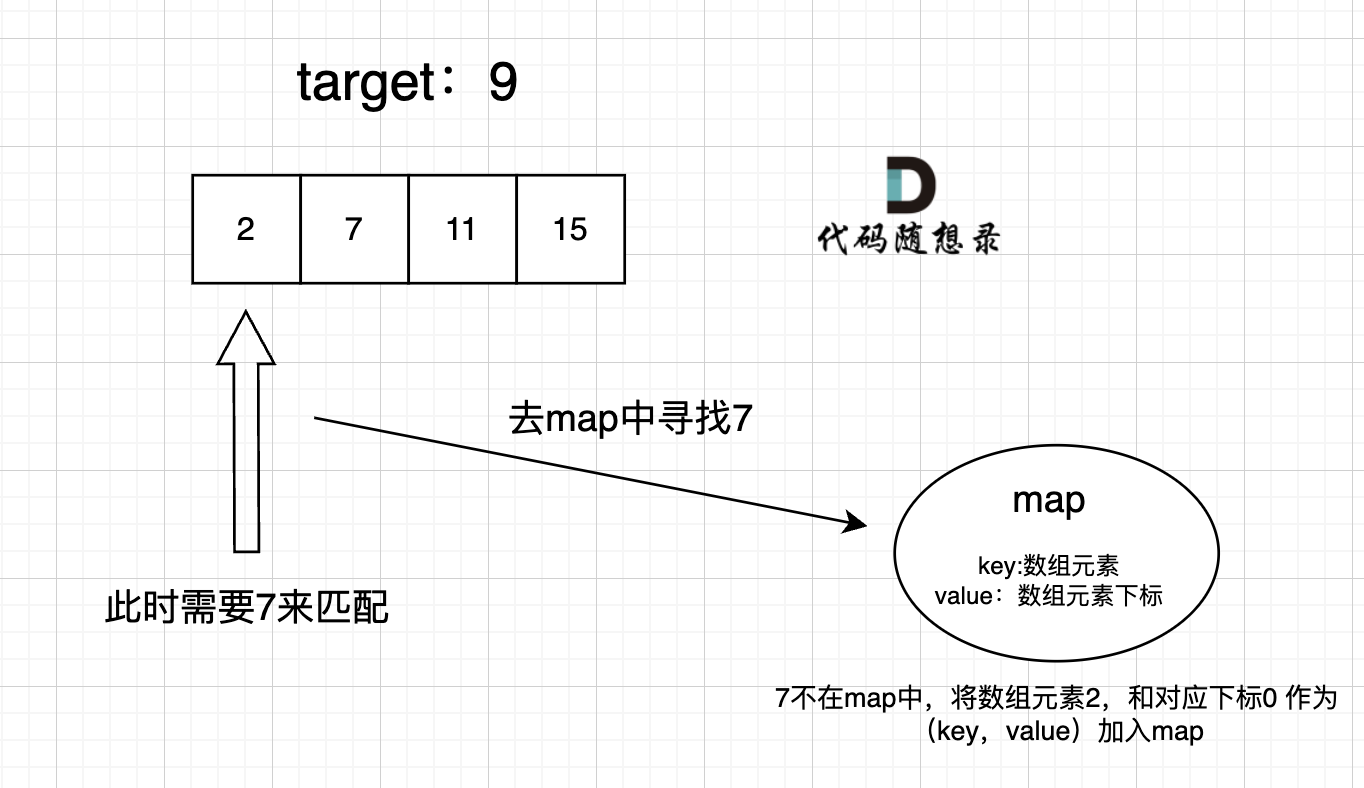
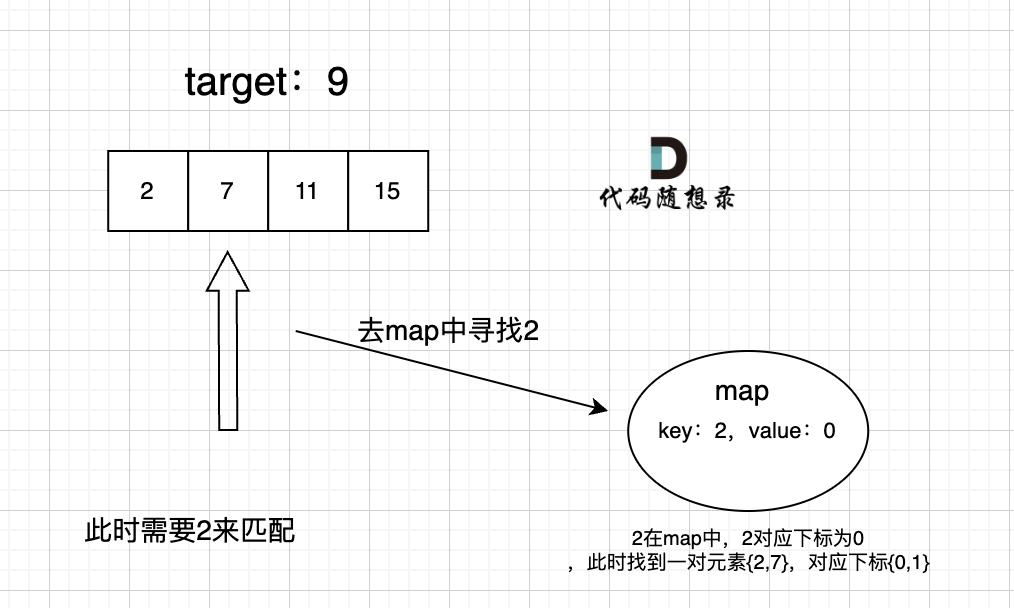
// hash:key存储值,value存储下标
public static int[] twoSum1(int[] nums, int target) {
HashMap<Integer, Integer> map = new HashMap<>();
int[] res = new int[2];
for (int i = 0; i < nums.length; i++) {
// target - nums[i] 作为key用来查找,map中有直接返回
if (map.containsKey(target - nums[i])) {
res[0] = i;
res[1] = map.get(target - nums[i]);
}else {
map.put(nums[i],i);
}
}
return res;
}
15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
思路分析
首先第一想法肯定也是暴力法,使用三层for循环,逐个遍历。但是题目中有个很关键的条件,三元组不能重复,但是每组结果里面的元素是可以重复的,如果使用暴力法,再去考虑去重,时间、空间非常的高,并不容易实现。
使用hash法呢? 使用俩层for循环,然后尝试获取 0 - a - b 。 使用hash算法去重的操作也是很麻烦的。
因此可以使用双指针算法,使用一层 for 循环,i 指向数组第一个元素,left 指向 i+1 的位置上,right指向末尾元素。
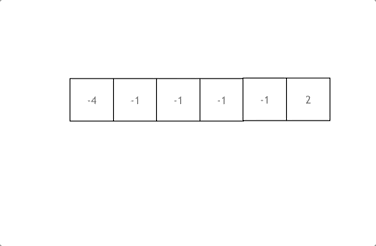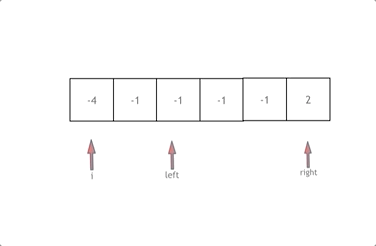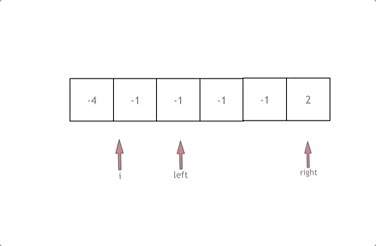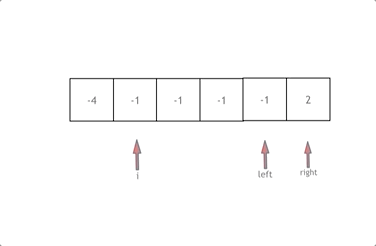
- 先对数组进行排序
- 其次计算 $nums[i] + nums[left] + nums[right] $的和 sum
- 若 sum < 0, 说明元素较小,将 left 右移
- 若 sum > 0 , 说明元素较大,将right 左移
- 若 sum= 0 , i、left、right 则是一组解,加到集合中即可
基本的逻辑是这样,如何去重呢? 此时我就想到了能不能使用Set集合自动去重,不用我们手动去重呢,于是代码如下:
public static List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
// 使用set集合避免重复的三元组
Set<List<Integer>> res = new HashSet<>();
for (int i = 0; i < nums.length - 2; i++) {
// 处理特殊情况
if (nums[i] > 0) return res;
int left = i + 1;
int right = nums.length - 1;
while(left < right) {
if (nums[i] + nums[left] + nums[right] > 0) {
// 元素值太大,将right左移
right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
// 元素值太小,将left右移
left++;
} else {
// 相等
List<Integer> item = new ArrayList<>();
item.add(nums[i]);
item.add(nums[left]);
item.add(nums[right]);
res.add(item);
// 找到一组解之后,同时移动
right--;
left++;
}
}
}
return new ArrayList<List<Integer>>(res);
}
这种方法的耗时较高,因为把重复的元素也都计算了一遍,因此我们可以考虑跳过重复元素【相邻元素进行比较】,跳过重复元素也就没有必要使用 Set 集合了,使用普通集合即可。代码如下:
public static List<List<Integer>> threeSum1(int[] nums) {
ArrayList<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length-2; i++) {
// 处理特殊情况
if (nums[i] > 0) return res;
int left = i+1;
int right = nums.length -1;
// 对i进行去重
/*
* 这里只能使用nums[i] == nums[i-1]
* 不能使用nums[i] == nums[i+1],因为 i+1 可能会丢失
* 比如:-1,-1,2 这种情况
* */
if (i>0 && nums[i] == nums[i-1]) continue;
while(left < right) {
if (nums[i] + nums[left] + nums[right] < 0) {
// 右移
left++;
}else if (nums[i] + nums[left] + nums[right] > 0) {
// 左移
right--;
}else {
res.add(Arrays.asList(nums[i],nums[left],nums[right]));
// 对 left、right去重
while(left < right && nums[left] == nums[++left]);
while(left < right && nums[right] == nums[--right]);
}
}
}
return res;
}
18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例 2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]
提示:
1 <= nums.length <= 200-109 <= nums[i] <= 109-109 <= target <= 109
思路分析
相较于三数之和,多了一层for循环,并且判断的条件值不在是0,而是 任意的 target。
因此不能在简单的判断 $nums[i] > target$ 就返回了,比如:[-4, -3, -2, -1],target是-10,不能因为-4 > -10而跳过。
更改条件为: nums[i] > target nums[i] > 0
五数、六数之和都是这个逻辑
代码如下:
// 相较于三数之和,多一层for循环
public static List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
ArrayList<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < nums.length-2; i++) {
// 特殊情况判断
if (nums[i] > 0 && nums[i] > target) return res;
// 对 i 进行去重
if (i > 0 && nums[i] == nums[i-1]) continue;
for (int j = i+1; j < nums.length-2; j++) {
// 对 j 去重
if (j > i+1 && nums[j] == nums[j-1]) continue;
int left = j+1;
int right = nums.length-1;
while(left < right) {
if (nums[i] + nums[j] + nums[left] + nums[right] < target){
// 右移
left++;
}else if (nums[i] + nums[j] + nums[left] + nums[right] > target) {
// 左移
right--;
}else {
res.add(Arrays.asList(nums[i],nums[j],nums[left],nums[right]));
// 对left、right去重
while (left < right && nums[left] == nums[++left]);
while (left < right && nums[right] == nums[--right]);
}
}
}
}
return res;
}
