图论

鲨瓜大约 16 分钟

图论

dfs 和 bfs 的区别

深度优先遍历(dfs): 顺着一个方向遍历，就像是不到黄河不回头，直到没有元素了，再换另一个方向继续遍历。

广度优先遍历(bfs): 先遍历与本节点连接的所有节点，然后在遍历与下一个节点相连接的所有节点

其实dfs就是回溯，当遍历到头时，就需要回溯换另一个方向继续遍历。在二叉树中的递归遍历其实就是 dfs，而迭代遍历就是 bfs。

下面通过俩张动图，体会一下dfs和bfs的区别：

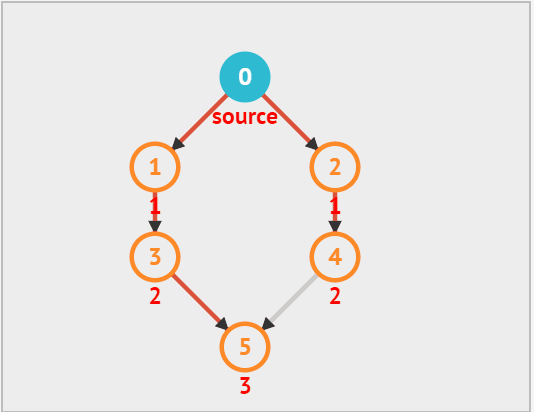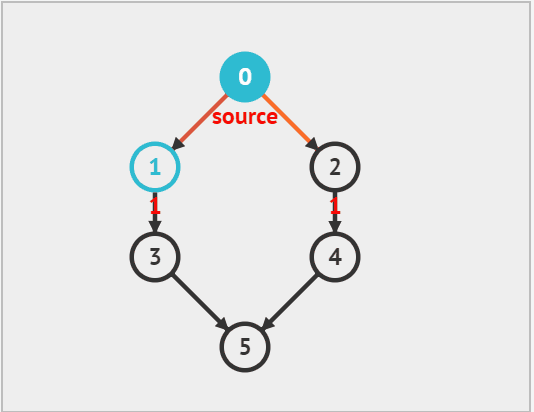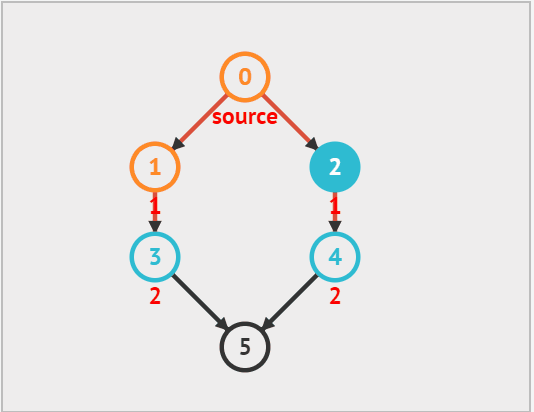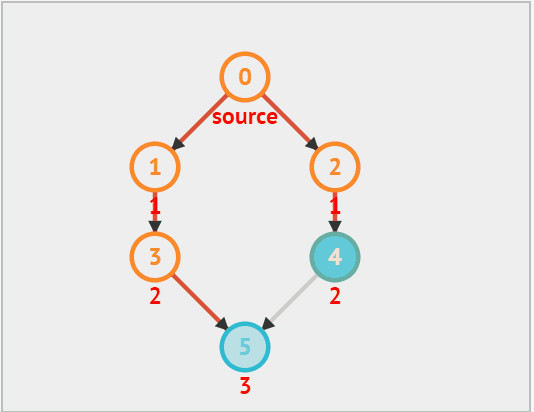
dfs：

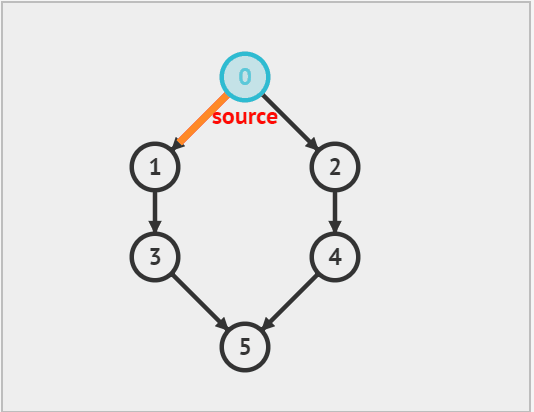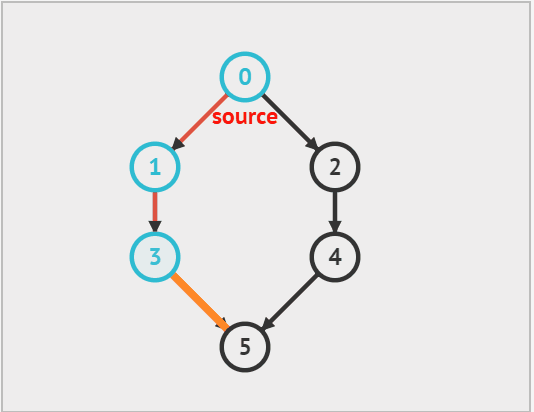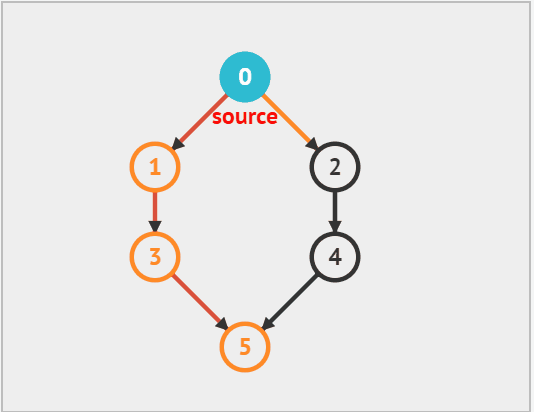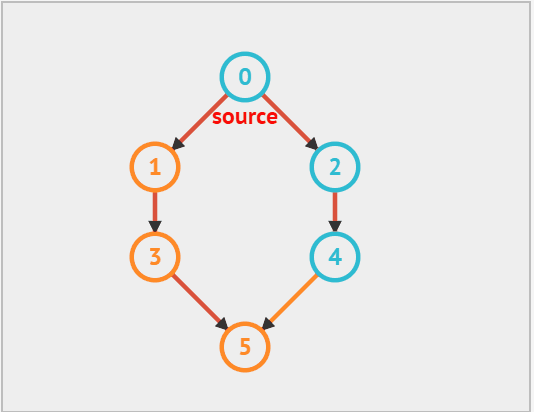
从上面的动态图中可以看出，每次向下搜索都是递归的过程，而 '换方向' 拿图中来说，从 5 换到了 2 就是回溯的过程，因此递归和回溯是相辅相成的。

再来回顾一下回溯算法的代码模板：

在回溯章节中，已经练习了大量的回溯算法，一般情况，深搜需要二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。

List<List<String>> res = new ArrayList<>();
List<String> path = new ArrayList<>();

void dfs(参数){
	if (终止条件){
		存放结果;
		return;
	}
	for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}
}

bfs:

BFS是一圈一圈的搜索过程，但具体是怎么一圈一圈来搜呢。

从某一个节点开始，先将该节点的上下左右四个方向的节点搜索出来，然后继续遍历下一个节点。

通常在 bfs 中需要使用一个容器来保存节点用来遍历。这个容器可以使用栈、队列、数组。

在这里我使用队列，这样遍历不用考虑遍历顺序的问题。用栈的话还要考虑先进后出的顺序。

除了容器之外，还需要一个 数组用来记录当前节点是否被访问过，在 dfs 中不需要是因为在搜索的过程中，每个节点在被访问时就被标记为已访问，而在回溯时会将标记清除，这样每个节点都只会被访问一次

总结起来，bfs做的步骤就是：入队 - 标记 - 出队 - 入队 - 标记.....

797. 所有可能的路径open in new window

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

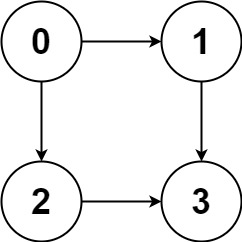
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

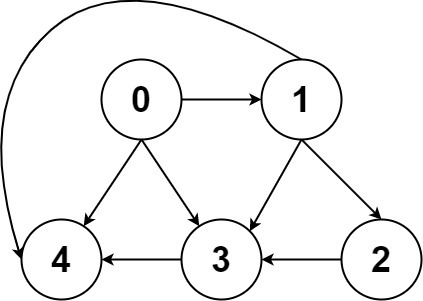
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图（DAG）

思路分析

dfs版本

在上面已经说过了，dfs就可以看做是回溯算法！因此我们直接套用回溯算法模板！

首先定义俩个集合，一个保存每一条路径，一个保存所有的路径

List<List<Integer>> allPath = new ArrayList<>();
List<Integer> path = new ArrayList<>();

确定返回值及参数

void dfs(graph,node)

终止条件

当前遍历的节点值等于图中最后一个元素值，就说明找到一条路径

if (node == graph.length()-1){
	allPath.add(path)
	return
}

单层递归逻辑

当前结点为 node，那么要找到与node相连接的下一个节点，则 graph[node] 就是与node所有相连的节点列表。

逐个将它加到path集合中，并往下递归，递归之后要进行回溯。每一次递归结束说明找到了一条路径。因此要回溯到上一个结点继续搜索

        // graph[node] 表示所有与node相连的节点列表
        for (int i = 0; i < graph[node].length; i++) {
            path.add(graph[node][i]);
            dfs(graph,graph[node][i]); // 递归，继续找与graph[node][i]相连的节点
            // 回溯：递归之前做了什么递归之后就要回溯
            path.remove(path.size()-1);
        }

完整代码

class Solution {
     List<List<Integer>> allPath = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
         path.add(0); // 不要忘记将0结点加入到路径当中
        dfs(graph,0);
        return allPath;
    }
    void dfs(int[][] graph,int node){
        if (node == graph.length-1) {
            // 说明找到了一条路径
            allPath.add(new ArrayList(path));
            return;
        }
        // graph[node] 表示所有与node相连的节点列表
        for (int i = 0; i < graph[node].length; i++) {
            path.add(graph[node][i]);
            dfs(graph,graph[node][i]); // 递归，继续找与graph[node][i]相连的节点
            // 回溯：递归之前做了什么递归之后就要回溯
            path.remove(path.size()-1);
        }
    }
}

200. 岛屿数量open in new window

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

思路分析

dfs

遍历数组，如果当前值为1，将岛屿数量+1，并且进入到感染函数里。

感染函数：其实就是一个递归标注的过程，它会将所有相连的1都标注成2。为什么要标注？这样就避免了遍历过程中的重复计数的情况，一个岛所有的1都变成了2后，遍历的时候就不会重复遍历了。

class Solution {
    public int numIslands(char[][] grid) {
        int landNums = 0; // 岛屿数量
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == '1') {
                    landNums++;
                    infect(grid, i, j);
                }
            }
        }
        return landNums;
    }

    // 感染函数，目的就是将相连的岛屿进行标记，避免重复计算
    private void infect(char[][] grid, int i, int j) {
        if (i < 0 || i >= grid.length ||
                j < 0 || j >= grid[0].length || grid[i][j] != '1') {
            return;
        }
        // 标记当前陆地
        grid[i][j] = '2';
        infect(grid, i + 1, j);
        infect(grid, i - 1, j);
        infect(grid, i, j + 1);
        infect(grid, i, j - 1);
    }
}

bfs

    public int numIslandsBFS(char[][] grid) {
        int landNums = 0; // 岛屿数量
        visited = new boolean[grid.length][grid[0].length];

        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == '1' && !visited[i][j]) {
                    landNums++;
                    infectBFS(grid, i, j);
                }
            }
        }
        return landNums;
    }

    // 标记是否被访问
    boolean[][] visited;
    // 上下左右四个方向
    int[][] move = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    // bfs 感染函数
    public void infectBFS(char[][] grid, int i, int j) {
        Queue<int[]> queue = new ArrayDeque<>();
        // 入队
        queue.offer(new int[]{i, j});
        // 标记
        visited[i][j] = true;

        while(!queue.isEmpty()) {
            // 出队
            int[] poll = queue.poll();
            int x = poll[0];
            int y = poll[1];
            // 向四个方向移动
            for (int k = 0; k < 4; k++) {
                int nextX = x + move[k][0];
                int nextY = y + move[k][1];
                // 下标越界，跳过
                if (nextX < 0 || nextX >= grid.length || nextY <0 || nextY >= grid[0].length) continue;
                if (!visited[nextX][nextY] && grid[nextX][nextY] == '1') {
                    queue.offer(new int[]{nextX, nextY});
                    visited[nextX][nextY] = true;
                }
            }
        }
    }

695. 岛屿的最大面积open in new window

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

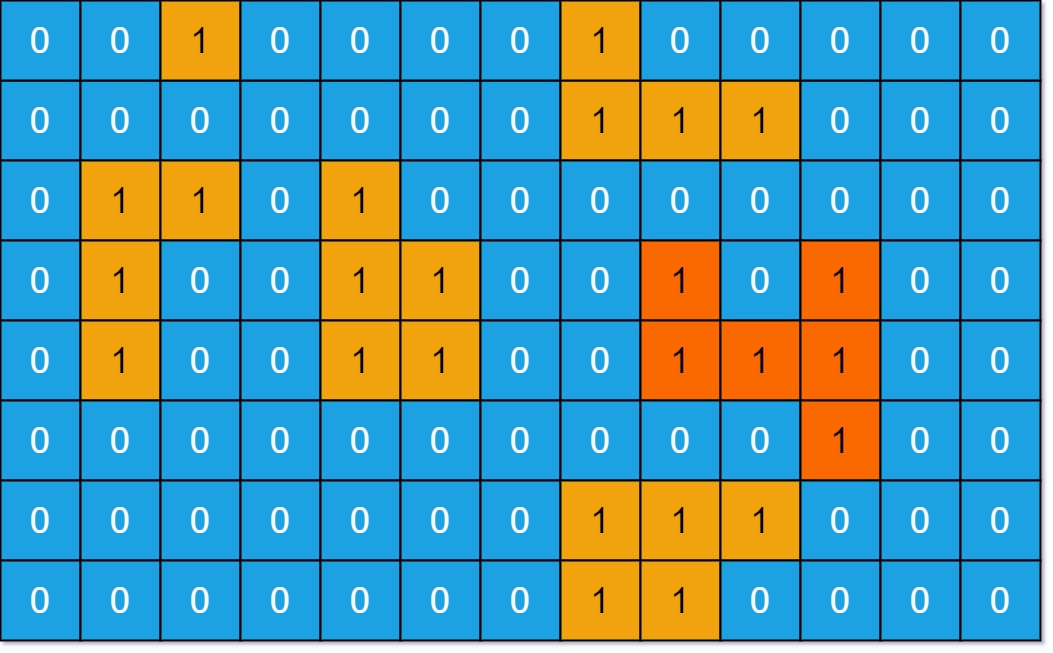
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

思路分析

和200. 岛屿数量open in new window一样，只不过在每次 "感染" 陆地时，记录一下陆地的数量。

dfs

    int area = 0;
    public int maxAreaOfIsland(int[][] grid) {
        int maxArea = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == 1) {
                    // 记录每块陆地的面积
                    area = 0;
                    infect(grid,i,j);
                    // 记录最大面积
                    maxArea = Math.max(maxArea,area);
                }
            }
        }
        return maxArea;
    }
    // dfs 感染函数: 将每块陆地 "感染"，避免重复计算
    public void infect(int[][] grid, int x, int y) {
        if (x < 0 || y < 0 || x >= grid.length || y >= grid[x].length || grid[x][y] != 1) return;
        grid[x][y] = 2;
        area++; // 将当前陆地的面积+1
        infect(grid, x + 1, y);
        infect(grid, x - 1, y);
        infect(grid, x, y - 1);
        infect(grid, x, y + 1);
    }

bfs

    boolean[][] visited;
    int[][] move = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
     int area = 0;
    public int maxAreaOfIslandBFS(int[][] grid) {
        visited = new boolean[grid.length][grid[0].length];
        int maxArea = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == 1 && !visited[i][j]) {
                    area = 0;
                    infectBFS(grid,i,j);
                    // 记录最大面积
                    maxArea = Math.max(maxArea,area);
                }
            }
        }
        return maxArea;
    }
        // bfs
    public void infectBFS(int[][] grid, int x, int y) {
        Queue<int[]> queue = new ArrayDeque<>();
        queue.offer(new int[]{x,y});
        visited[x][y] = true;
        area++;
        while(!queue.isEmpty()) {
            int[] poll = queue.poll();
            int i = poll[0];
            int j = poll[1];
            for (int k = 0; k < 4; k++) {
                int nextX = i + move[k][0];
                int nextY = j + move[k][1];
                if (nextX < 0 || nextY < 0 || nextX > grid.length || nextY >= grid[0].length ) continue;

                if (!visited[nextX][nextY] && grid[nextX][nextY] == 1) {
                    area++;
                    queue.offer(new int[]{nextX, nextY});
                    visited[nextX][nextY] = true;
                }
            }
        }
    }

1020. 飞地的数量open in new window

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

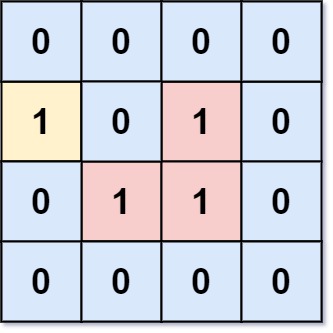
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

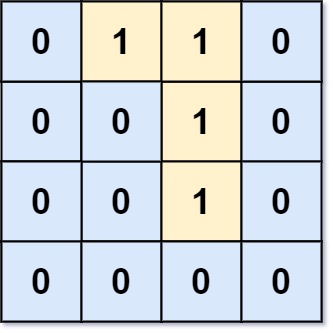
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0 或 1

思路分析

题目要求不与边界相连的陆地单元格的数量，那么我们应该利用 "感染" 函数将边界陆地都 "感染" 为海洋，然后在统计陆地单元格的数量

dfs

class Solution {
    public int numEnclaves(int[][] grid) {
        int rowLength = grid.length;
        int colLength = grid[0].length;

        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                // 将靠近边界的陆地都变成海洋
                if ((i == 0 || j == 0 || i == rowLength - 1 || j == colLength - 1) && grid[i][j] == 1)
                    infect(grid, i, j);
            }
        }
        int landNums = 0;
        // 统计陆地单元格的数量
        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                    if (grid[i][j] == 1) landNums++;
            }
        }
        return landNums;
    }

    // 感染函数
    public void infect(int[][] grid, int x, int y) {
        if (x < 0 || y < 0 || x >= grid.length || y >= grid[x].length || grid[x][y] == 0) return;
        // 将陆地变成海洋
        grid[x][y] = 0;

        infect(grid, x - 1, y);
        infect(grid, x + 1, y);
        infect(grid, x, y - 1);
        infect(grid, x, y + 1);
    }
}

bfs

这道题无需使用 visited 数组，不关心他是否重复访问，只要将边界的陆地变为海洋即可。

class Solution {
    int[][] move  = {{0,1},{0,-1},{1,0},{-1,0}};

    public int numEnclaves(int[][] grid) {
       int rowLength = grid.length;
        int colLength = grid[0].length;

        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                // 将靠近边界的陆地都变成海洋
                if ((i == 0 || j == 0 || i == rowLength - 1 || j == colLength - 1) && grid[i][j] == 1 )
                    infectBFS(grid, i, j);
            }
        }
        int landNums = 0;
        // 统计陆地单元格的数量
        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                if (grid[i][j] == 1) landNums ++;
            }
        }
        return landNums;
    }

        public void infectBFS(int[][] grid, int x, int y){
        Queue<int[]> queue = new ArrayDeque<>();

        queue.offer(new int[]{x,y});
        grid[x][y] = 0;

        while(!queue.isEmpty()) {
            int[] poll = queue.poll();
            int m = poll[0];
            int n = poll[1];
            // 遍历四个方向
            for (int i = 0; i < 4; i++) {
                int nextX = m + move[i][0];
                int nextY = n + move[i][1];

                if (nextX < 0 || nextY < 0 || nextX >= grid.length || nextY >= grid[nextX].length ) continue;
                
                if (grid[nextX][nextY] == 1) {
                    queue.offer(new int[]{nextX,nextY});
                     grid[nextX][nextY] = 0;
                }
            }

        }
    }
}

130. 被围绕的区域open in new window

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

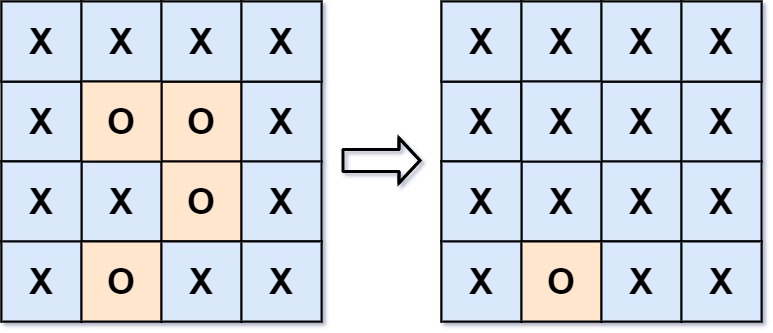
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

思路分析

和 1020. 飞地的数量open in new window 思路一样，先将与边界相连的陆地，也就是O变成另外一个字符，比如我变成 A。遍历数组，将O变成X，将A变成O

dfs

class Solution {
    public void solve(char[][] board) {
        int rowLength = board.length;
        int colLength = board[0].length;

        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                // 将靠近边界的O都改为A
                if ((i == 0 || j == 0 || i == rowLength - 1 || j == colLength - 1) && (board[i][j] == 'O') )
                    infect(board, i, j);
            }
        }

        // 将图中的O改为X，A改为A
        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                if (board[i][j] == 'O')
                    board[i][j] = 'X';

                if (board[i][j] == 'A')
                    board[i][j] = 'O';
            }
        }
    }

    // 感染函数
    public void infect(char[][] board, int x, int y) {
        if (x < 0 || y < 0 || x >= board.length || y >= board[x].length || board[x][y] == 'A' ||board[x][y] == 'X' ) return;
        board[x][y] = 'A';

        infect(board, x - 1, y);
        infect(board, x + 1, y);
        infect(board, x, y - 1);
        infect(board, x, y + 1);
    }
}

bfs

class Solution {
    int[][] move  = {{0,1},{0,-1},{1,0},{-1,0}};

    public void solve(char[][] board) {
        int rowLength = board.length;
        int colLength = board[0].length;

        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                // 将靠近边界的O都改为A
                if ((i == 0 || j == 0 || i == rowLength - 1 || j == colLength - 1) && board[i][j] == 'O')
                    infectBFS(board, i, j);
            }
        }
        // 将图中的O改为X，A改为A
        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                if (board[i][j] == 'O')
                    board[i][j] = 'X';

                if (board[i][j] == 'A')
                    board[i][j] = 'O';
            }
        }
    }

        public void infectBFS(char[][] board, int x, int y){
        Queue<int[]> queue = new ArrayDeque<>();

        queue.offer(new int[]{x,y});
        board[x][y] = 'A';


        while(!queue.isEmpty()) {
            int[] poll = queue.poll();
            int m = poll[0];
            int n = poll[1];
            // 遍历四个方向
            for (int i = 0; i < 4; i++) {
                int nextX = m + move[i][0];
                int nextY = n + move[i][1];

                if (nextX < 0 || nextY < 0 || nextX >= board.length || nextY >= board[nextX].length || board[nextX][nextY] == 'X') continue;

                if ( board[nextX][nextY] == 'O' ) {
                    queue.offer(new int[]{nextX,nextY});
                    board[nextX][nextY] = 'A';
                }
            }
        }
    }
}

417. 太平洋大西洋水流问题open in new window

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

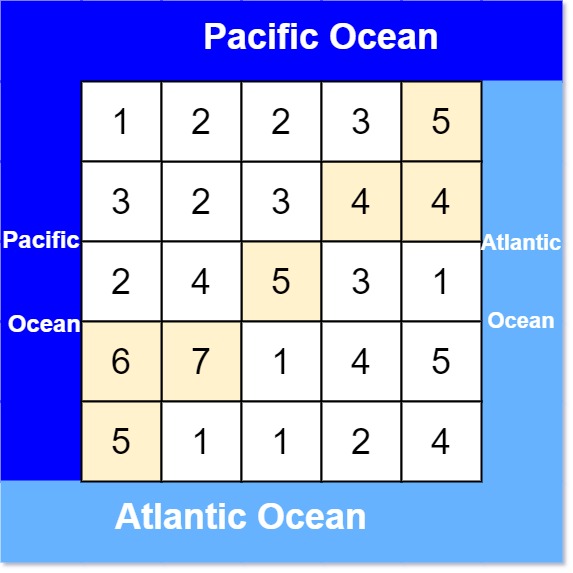
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 105

思路分

该题目求：大西洋和太平洋都能够到达的坐标

我们可以逆向分析，先从太平洋出发找到能够到达的坐标，将其标记，然后再从大西洋出发找到能够到达的坐标，将其标记。

同时被标记的就是都能够到达的坐标

dfs

class Solution {
    int[][] move = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    int rowLength, colLength;

    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        List<List<Integer>> res = new ArrayList<>();
        rowLength = heights.length;
        colLength = heights[0].length;

        // 保存太平洋可以到达的地点
        boolean[][] pacific = new boolean[rowLength][colLength];
        // 保存大西洋可以到达的地点
        boolean[][] atlantic = new boolean[rowLength][colLength];

        for (int i = 0; i < rowLength; i++) {
            infect(heights, i, 0, pacific); // 左边界
            infect(heights, i, colLength - 1, atlantic);// 右边界
        }

        for (int i = 0; i < colLength; i++) {
            infect(heights, 0, i, pacific); // 上边界
            infect(heights, rowLength - 1, i, atlantic); // 下边界
        }
        


        for (int i = 0; i < rowLength; i++) {
            for (int j = 0; j < colLength; j++) {
                if (atlantic[i][j] && pacific[i][j]) {
                    // 大西洋、太平洋同时可以到达的地点
                    ArrayList<Integer> list = new ArrayList<>();
                    list.add(i);
                    list.add(j);
                    res.add(list);
                }
            }
        }
        return res;
    }

    // 感染函数
    public void infect(int[][] heights, int x, int y, boolean[][] ocean) {
        // 地点已被标记,结束递归
        if (ocean[x][y]) return;
        ocean[x][y] = true;

        for (int i = 0; i < 4; i++) {
            int nextX = x + move[i][0];
            int nextY = y + move[i][1];
            // 边界条件，
            // heights[x][y]当前单元格高度
            // heights[nextX][nextY] 相连单元格高度
            // 如果相连的单元格高度小于当前单元格高度，说明它到不了当前单元格(因为是由低->高)，因此跳过！
            if (nextX < 0 || nextY < 0 || nextX >= rowLength || nextY >= colLength || heights[x][y] > heights[nextX][nextY])
                continue;

            infect(heights, nextX, nextY, ocean);
        }
    }
}

昵称

邮箱

网址

按正序
按倒序
按热度

图论

预览: