数组
数组
217 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1]
输出:true
示例 2:
输入:nums = [1,2,3,4]
输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true
思路分析
题比较简单,实现思路也有很多。
- 可以转换成一个 Set 集合,因为 set 集合是不重复的。通过对比转换前后的长度就可以得知是否重复
- 也可以先对数组进行排序,重复的肯定是相邻的俩个数,挨个比对判断就行了。
- 使用 Jdk8 中 的 Stream流,通过去重操作,然后收集去重后的数据,比对长度即可。
代码实现
由于题比较简单,就写出第三种方式的代码。
/*
* 利用JDK8的新特性,对nums数组进行去重操作,统计去重后数组的长度
* 比原来数组小就说明有重复的,反之则没有
* */
public static boolean containsDuplicate(int[] nums) {
long count = Arrays.stream(nums).distinct().count();
return !(count == nums.length);
}
704 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
思路分析
二分查找是一个简单,但是一个非常经典的搜索算法,但是经常会将 while 条件搞混,例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?
混淆的原因主要是区间没有定义好,在二分查找中一般有俩个常用的区间:
- 左闭右闭 :[ left, right ]
- 左闭右开 : [ left, right )
代码实现
第一种写法:左闭右闭
确定好了左闭右闭区间,这就决定了我们如何写 while 条件以及right 的变化:
while (left <= right)要使用 <= ,因为left == right是有意义的,所以使用 <=if (nums[middle] > target) right = middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是middle - 1
// 定义区间: [left,right]
public static int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
// 因为我们定义的是左闭右闭区间, left == right 是有意义的
while (left <= right) {
// 找出中间索引
int middle = (left + right) / 2;
if (nums[middle ] > target) {
// 这里使用 middle-1,因为在 if 中已经判断了 middle 处的值一定不是 target
// 因此在 middle-1 为终止条件
right = middle - 1;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
return -1;
}
第二种:左闭右开区间
while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的if (nums[middle] > target) right = middle,在 if 中同样能看出,nums[middle]一定不等于 target,因此需要从middle -1作为结束索引,但是在[left,middle)中,已经不包含 middle ,因此就无需 -1 。
// 定义区间: [left,right)
public static int search(int[] nums, int target) {
int left = 0;
int right = nums.length;
// 因为我们定义的是左闭右开区间, left == right 是不成立的
while (left < right) {
// 找出中间索引
int middle = (left + right) / 2;
if (nums[middle ] > target) {
// 这里使用 middle,是因为 [left,middle) 中已经不包含了 middle。
right = middle ;
}else if (nums[middle] < target) {
left = middle + 1;
}else {
return middle;
}
}
return -1;
}
相关题目
35 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 无重复元素 的 升序 排列数组-104 <= target <= 104
思路分析:
在分析该题目时,不要太在意 左闭右开、左闭右闭区间 ,而是应该具体问题具体分析,根据题意确定 left、right 以及 mid 与 target的关系 的变化
通过题目可以得知:要求返回第一个大于等于 target 的元素位置
情况一: 如果 nums[mid] 小于 target 的值, 那么 mid 以及 mid 左边所有的位置都不符合题意。因此需要向右移动 left = mid + 1
情况二:如果 nums[mid] 大于 target 的值,那么 mid 右边所有的位置肯定不符合题意,因此需要向左移动:right = mid,并且 mid 有可能是需要返回的位置, 但前提是 mid 左边的所有元素都不符合题意。也就是说 mid 左边的所有元素都小于或者不等于 target
代码
public static int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length;
int mid = 0;
while (left < right) {
mid = (left + right) / 2;
// 如果 nums[mid] < target 说明,mid及mid左边的所有位置都不符合题意
if (nums[mid] < target) {
left = mid + 1;
} else {
// 相反如果等于 nums[mid] >= target, 此时说明 mid 有可能是需要返回的位置
// 但前提是 mid 左边的所有元素都不符合题意。也就是说 mid 左边的所有元素都小于或者不等于 target
right = mid;
}
}
return left;
}
}
第二种思路:
题目中重要的俩个条件:1、升序 2、无重复元素
我们可以得知,在找到 target 合适的位置 i 时 ,那么它一定满足以下的条件:$ target >= nums[0]...nums[i-1]$
我们就可以利用这个条件,不使用二分查找,直接使用 for 循环。
代码如下:
public int searchInsert(int[] nums, int target) {
// 升序、无重复元素,只要某个元素大于target值,该元素的位置就是就是要返回的值
if(nums.length == 0) return -1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] >= target) return i;
}
// 循环结束仍然没有位置,说明 target 在数组中是最大的,直接插入数组末尾即可。
return nums.length;
}
278. 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例 1:
输入:n = 5, bad = 4
输出:4
解释:
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
示例 2:
输入:n = 1, bad = 1
输出:1
提示:
1 <= bad <= n <= 231 - 1
思路分析
题目要求和 35 题一样,该题是求出第一个错误版本。但是有一个小坑。
int类型最大值为 2^31 - 1 , 这里如果单纯的使用: mid = (left + right) / 2; 可能会造成溢出
因此使用:left + (right - left) / 2;
public int firstBadVersion(int n) {
int left = 1;
int right = n;
while(left < right) {
int mid = left + (right - left) / 2;
if (!isBadVersion(mid)) {
// 当前mid版本没有错误,说明mid及mid之前都没有错误,
left = mid + 1;
}else {
// 相反,mid出错,可能是mid是第一个出错的,也可能是mid前面版本出错
right = mid;
}
}
return left;
}
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
思路分析
第一种方法: 直接遍历
第一次遍历找到第一个相等的元素下标,第二次遍历找到最后一个相等元素的下标
public int[] searchRange(int[] nums, int target) {
int start = -1;
int end = -1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == target) {
start = i;
end = i;
break;
}
}
if (start == -1) return new int[]{start,end};
for (int i = start; i < nums.length; i++) {
if (nums[i] != target) break;
end++;
}
return new int[]{start,end};
}
第二种方法:二分法
通过二分法找到相等的元素后,向左继续搜索找到开始下标,向右继续搜索找到结束下标
class Solution {
public int[] searchRange(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
while(left<=right){
int mid = left+(right-left)/2;
if(nums[mid]==target){
// 向两边扩张
int l = mid;
while(l>=left&&nums[l]==target){
l--;
}
int r = mid;
while(r<=right&&nums[r]==target){
r++;
}
return new int[]{++l,--r};
}else if(nums[mid]>target){
//左边
right = mid-1;
}else{
left = mid+1;
}
}
return new int[]{-1,-1};
}
}
153. 寻找旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
思路分析
根据题意得知:
输入数组是一个不重复的升序数组旋转 1~n 次得到的,具体旋转咱也不知道,但是不管旋转几次,肯定是有一部分是有序的,并且最小值一定是在无序的那部分上。因此可以利用二分法找无序的那一部分。
- $nums[mid] > nums[right]$ , 说明最小值在右半边,舍弃左半边。即:
left = mid + 1;- 这里为什么是
left = mid + 1;而不是left = mid呢? 这是因为mid一定不是最小的,至少nums[right]比它小
- 这里为什么是
- $nums[mid] <= nums[right]$ , 说明最小值在左半边,舍弃右半边,即:
right = mid;- 这里 mid 有可能是最小值,因此保留mid的取值
代码实现
// 使用二分法
public int findMin1(int[] nums) {
int low = 0;
int high = nums.length -1 ;
while (low < high) {
int mid = (low + high) /2 ;
if (nums[mid] < nums[high]) {
// 如果中间值小于最大值,那么就抛弃右区间
high = mid;
}else{
// 否则抛弃左区间
low = mid + 1;
}
}
return nums[low];
}
疑问:
1、为什么要使用 $low < high$ , 使用 $low <= high$ 不行嘛?
其实是可以的,但是需要多考虑一些情况,如果是 <= 的话,当 low=high时,还要执行一遍循环。
如下图所示,此时 low=high,符合条件,仍需要执行一遍 low = mid - 1,此时 low = -1。所以当使用 <= 时,返回值有俩种写法:
- return nums[low+1]
- return nums[high]
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104nums中的每个值都 独一无二- 题目数据保证
nums在预先未知的某个下标上进行了旋转 -104 <= target <= 104
思路分析
题目要求 O(logN)的时间复杂度,基本可以断定本题是需要使用二分查找,怎么分是关键。由于题目说数字了无重复,举个例子:1 2 3 4 5 6 7可以大致分为两类,
第一类 2 3 4 5 6 7 1 这种,也就是 nums[left] <= nums[mid]。此例子中就是 2 <= 5。
- 这种情况下,前半部分有序。因此如果 nums[left] <=target<nums[mid],则在前半部分找,否则去后半部分找。
第二类 6 7 1 2 3 4 5 这种,也就是 nums[left] > nums[mid]。此例子中就是 6 > 2。
- 这种情况下,后半部分有序。因此如果 nums[mid] <target<=nums[right],则在后半部分找,否则去前半部分找。
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] >= nums[left]) { // 中间值>最左边的值,说明左半段是有序的
if (target >= nums[left] && target < nums[mid]) { // 判断目标值在中间值的左边还是右边,以此调整left和right
// 在左边,需要舍弃右边
right = mid - 1;
} else {
// 在右边,需要舍弃左边
left = mid + 1;
}
} else { // 中间值 < 最左边的值,说明右半段是有序的
if (target <= nums[right] && target > nums[mid]) {
left = mid + 1;
}else {
right = mid - 1;
}
}
}
return -1;
}
}
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以**「引用」**方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
思路分析
此题看着并不难,实际考察的是你对数据底层的一个存储原理。很多人,包括我自己,在初始认为只需要遍历数组,将指定值删除即可, 这时你就会掉入了一个误区。因为数组中的存储空间是连续的,一经开辟,是无法删除的,只能将后边的元素往前移覆盖
双指针法
首先需要确定是双指针的含义(一般来说对于数组使用双指针,一个用来遍历,一个用来执行具体操作。):
fast 指针: 指向可以输出的元素
slow指针:指向被替换(删除)的元素【等于val的元素】
其次定义双指针如何移动:
- 如果 fast 指针指向不等于 val 的元素 ,就说明该元素是
输出元素,不用替换的元素。此时就将 fast 指向的元素替换掉 slow 指向的元素,完整"删除"操作。同时将 slow 指针向右移动。 - 如果 fast 指针指向等于val的元素,就说明该元素是需要被替换的元素,此时 slow 指针不动, fast 指针继续向右移动,直到找到一个输出元素。
具体的流程:
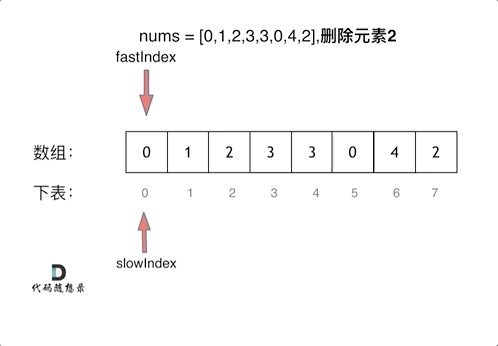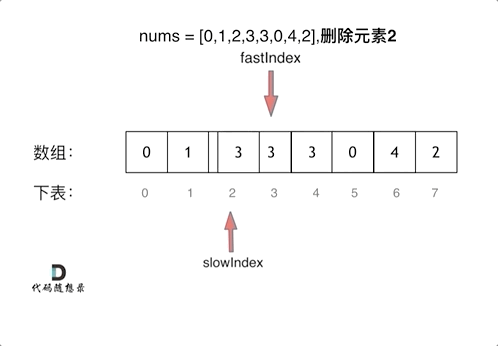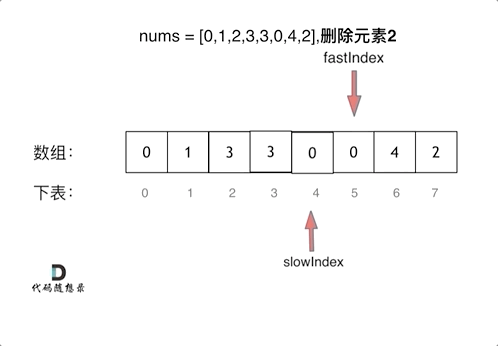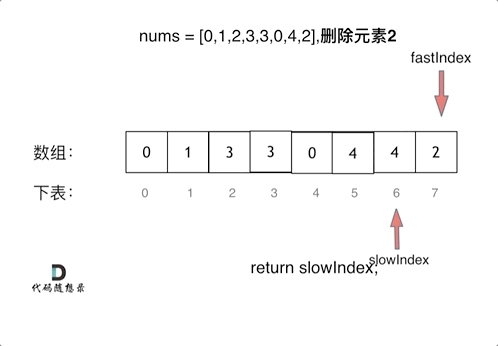 、
、
代码实现
/*
* 采用双指针:
* fast:指向输出元素【!= val的元素】
* slow:指向被替换的元素 【== val的元素】
* 当前元素是输出元素时,将fast指向的元素替换掉slow指向的元素。并移动双指针
* 当前元素不是输出元素时:只需要移动fast指针
* */
public static int removeElement(int[] nums, int val) {
// 定义双指针
int slow = 0;
for (int fast = 0; fast < nums.length; fast++) {
// 找到输出元素
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
}
// 遍历检查
// for (int i = 0; i < slow; i++) {
// System.out.println(nums[i]);
// }
// 此时 slow 就是新数组的长度
return slow;
}
977 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
思路分析
从题目可以得知,原始数组是递增的,并且平方后的数组也要求是递增。
暴力法:遍历数组,将每个数平方,然后将数组排序。
双指针法:
- 从题目可以得知,平方后最大的数不是在第一位【负数平方后变正数】就是最后一位。
- 因此可以利用双指针 i ,j ,i 指向数组首端,j指向尾端。
- 循环比较俩个数的值,将较大的数,放入一个新数组尾端【递增】,同时移动指向较大数的指针。
if (nums[i] * nums[i] < nums[j] * nums[j]) result [k--] = nums[j] * nums[j]
if (nums[i] * nums[i] >= nums[j] * nums[j]) result [k--] = nums[i] * nums[i]
效果图来源于代码随想录:代码随想录 (programmercarl.com)

代码实现
暴力法:
public static int[] sortedSquares(int[] nums) {
for (int i = 0; i < nums.length; i++) {
nums[i] *= nums[i];
}
// 重新排序
Arrays.sort(nums);
return nums;
}
双指针法:
// 双指针法
public static int[] sortedSquares(int[] nums) {
// 定义双指针
int i = 0;
int j = nums.length -1 ;
// 新数组
int[] result = new int[nums.length];
// 新数组指针
int k = j;
// i 超过 j指针时,循环结束
while (i <= j) {
// 将较大的数,放入新数组的尾端
if (nums[i] * nums[i] < nums[j] * nums[j]) {
result[k--] = nums[j] * nums[j];
j--;
}else {
result[k--] = nums[i] * nums[i];
i++;
}
}
return result;
}
209 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
思路分析
暴力法:
我直接想到的方法就是暴力法,通过俩层 for 循环,第一层循环是以某个元素为起始位置,第二层循环是以符合条件的终止位置。
滑动窗口:
所谓的滑动窗口,其实就是双指针,通过调节双指针的位置,确定滑动窗口的范围。在此范围内保证所有元素的和都 >= target
代码实现
// 双指针法: 滑动窗口
public static int minSubArrayLen(int target, int[] nums) {
int result = Integer.MAX_VALUE;
// left 指向滑动窗口起始位置
int left = 0;
int sum = 0;
// 通过for循环,将 right 指针移动到滑动窗口终止的位置
for (int right = 0; right < nums.length; right++) {
// sum 保存的是移动窗口内所有元素的和
sum += nums[right];
while (sum >= target){
// 符合条件
// 始终记录子数组的最小长度
result = Math.min(result,(right -left + 1));
// 由于left指针向右移动了一位,移动窗口缩小,因此sum也要减去移动的元素值
sum -= nums[left];
// 移动窗口
left++;
}
}
return result==Integer.MAX_VALUE ? 0: result;
}
59 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
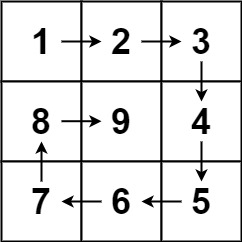
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
思路分析
矩阵的创建流程分俩种情况,第一种是偶数的情况,第二种是奇数的情况,如果是奇数,只需在循环结束后将矩阵中间的位置设置为最大值。因为最终都是到矩阵中间的位置结束。
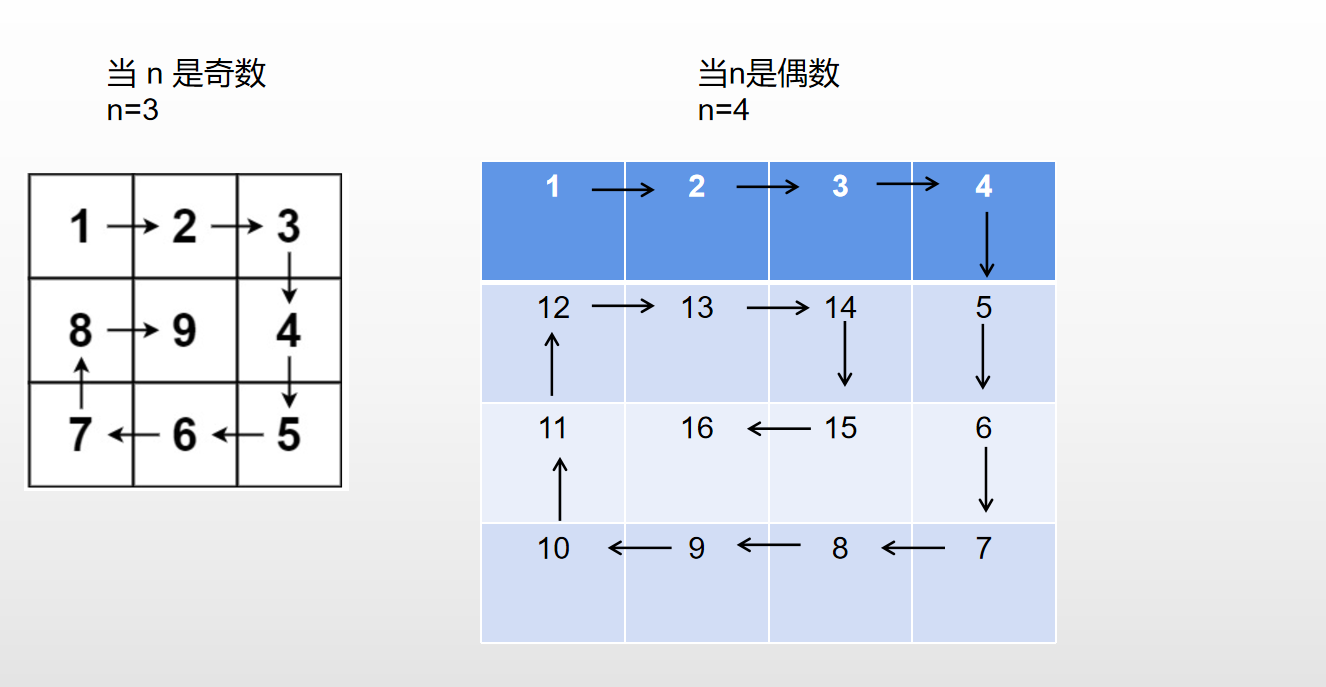
模拟顺时针画矩阵的过程:
- 顶层从左到右
- 右列从上到下
- 底层从右到左
- 左列从下到上
由外向内一圈圈的画下去
1、首先最重要的就是要确定 画矩阵 统一的规则,并且在画每一边时都要遵循这个规则。
比如:采取左闭右开 的原则,每一边都留下最后一个元素,留给下一条边处理。这样在处理的过程中就不会乱。
2、确定好规则,接下来就需要确定我们的循环的次数为:n/2 【如果不清楚,画一个找规律就知道为什么n/2了】
3、确定好循环次数,接下来就是对每一边进行处理。
代码实现
public static int[][] generateMatrix(int n) {
int loop = 0; // 控制循环次数
int[][] res = new int[n][n]; // 存放矩阵
int start = 0; // 每次循环的开始点(start, start)
int count = 1; // 定义填充数字
int i, j; // 模拟矩阵的行和列
while (loop++ < n / 2) { // 判断边界后,loop从1开始
// 模拟上侧从左到右
for (j = start; j < n - loop; j++) {
res[start][j] = count++;
}
// 模拟右侧从上到下
for (i = start; i < n - loop; i++) {
res[i][j] = count++;
}
// 模拟下侧从右到左
for (; j >= loop; j--) {
res[i][j] = count++;
}
// 模拟左侧从下到上
for (; i >= loop; i--) {
res[i][j] = count++;
}
// 每一次循环结束,下一次都会向里缩一圈。
// 所以起始位置+1
start++;
}
if (n % 2 == 1) {
res[start][start] = count;
}
return res;
}
1991 寻找数组的中心索引
给你一个下标从 0 开始的整数数组 nums ,请你找到 最左边 的中间位置 middleIndex (也就是所有可能中间位置下标最小的一个)。
中间位置 middleIndex 是满足 nums[0] + nums[1] + ... + nums[middleIndex-1] == nums[middleIndex+1] + nums[middleIndex+2] + ... + nums[nums.length-1] 的数组下标。
如果 middleIndex == 0 ,左边部分的和定义为 0 。类似的,如果 middleIndex == nums.length - 1 ,右边部分的和定义为 0 。
请你返回满足上述条件 最左边 的 middleIndex ,如果不存在这样的中间位置,请你返回 -1 。
示例 1:
输入:nums = [2,3,-1,8,4]
输出:3
解释:
下标 3 之前的数字和为:2 + 3 + -1 = 4
下标 3 之后的数字和为:4 = 4
示例 2:
输入:nums = [1,-1,4]
输出:2
解释:
下标 2 之前的数字和为:1 + -1 = 0
下标 2 之后的数字和为:0
示例 3:
输入:nums = [2,5]
输出:-1
解释:
不存在符合要求的 middleIndex 。
示例 4:
输入:nums = [1]
输出:0
解释:
下标 0 之前的数字和为:0
下标 0 之后的数字和为:0
提示:
1 <= nums.length <= 100-1000 <= nums[i] <= 1000
思路分析
看到这道题的首先第一个想法就是暴力法,假设第一个位置为 midIndex ,分别计算 midIndex 左边的和 与 右边的和,判断是否相等,相等则返回,不相等则 将 midIndex++, 指向下一个元素
代码实现
public int findMiddleIndex(int[] nums) {
// 特殊情况
if (nums.length == 1) return 0;
// 返回值值
int midIndex = 0;
while(midIndex < nums.length) {
// 分别保存左边和右边的和
int leftSum = 0;
int rightSum = 0;
// 左边和右边的指针
int left = 0;
int right = midIndex + 1;
// 计算左边的和
while (left < midIndex) {
leftSum += nums[left];
left++;
}
// 计算右边的和
while(right < nums.length) {
rightSum += nums[right];
right++;
}
// 如果相等返回 midIndex
if (rightSum == leftSum) return midIndex;
// 将midIndex继续指向下一个元素
midIndex++;
}
return -1;
}
优化
除了上面比较笨重的方法,在这里其实我们可以利用一个数学公式,已知 midIndex 左边与右边元素的和相等,假设用 leftSum 表示左边之和 , sum 表示 nums 数组总和,那么可以得出:
$leftSum = sum - leftSum - nums[midIndex]$
代码实现
public static int findMiddleIndex2(int[] nums) {
// 数组总和
int sum = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
}
int leftSum = 0;
for (int i = 0; i < nums.length; i++) {
if (leftSum == sum - leftSum - nums[i] ) return i;
leftSum += nums[i];
}
return -1;
}
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
思路分析
- 首先要按照每个区间的首元素进行升序
- 因为我们要根据首元素判断是否合并
- 其次我们需要一个额外的集合,将不合并的区间放入进去
- 判断是否可以合并
首先我们看如果俩个区间合并的话,需要满足以下的条件:
$$ intervals[i][0] <= intervals[i-1][1] (i >=1) $$
第 i 个区间的首元素小于或者等于 第 i-1 个区间的末尾元素,就说明可以合并,例如:
[1,4], [2,3] ==> [1,4]
[2,5],[3,8] ==> [2,8]
从上面例子中可以看出,如果进行合并的话,首元素就是俩个区间较小的那个,末尾元素则是俩个区间较大的那个。
代码实现
public static int[][] merge(int[][] intervals) {
// 结果集合
ArrayList<int[]> res = new ArrayList<>();
// 先对二维数组对初始元素进行排序
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
// 先将二维数组中第一个元素放到结果数组中
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
// 如果第二个区间的第一个元素 <= 结果集中最后一个区间的末尾元素,就进行合并
if (intervals[i][0] <= res.get(res.size() - 1)[1]) {
res.get(res.size() - 1)[1] = Math.max(intervals[i][1],res.get(res.size() - 1)[1]);
} else {
// 否则,直接加入结果数组中
res.add(intervals[i]);
}
}
return res.toArray(new int[res.size()][2]);
}
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
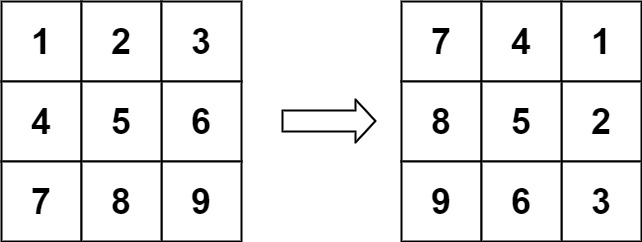
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
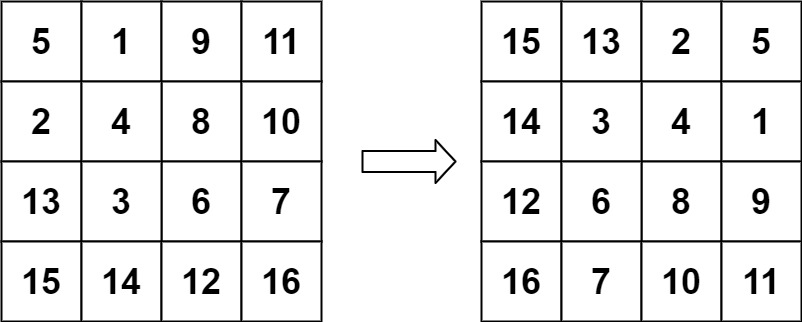
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
第一种方法:使用辅助矩阵
首先要知道如何旋转,每次旋转有什么规律,以例二为例:
在第一行旋转之后,变成了矩阵的最后一列:
比如:
- 第一个行第一个元素 ——》 倒数第一列第一个元素
- 第一个行第二个元素 ——》 倒数第一列第二个元素
- ....
在第二行旋转之后,变成了矩阵的倒数第二列:
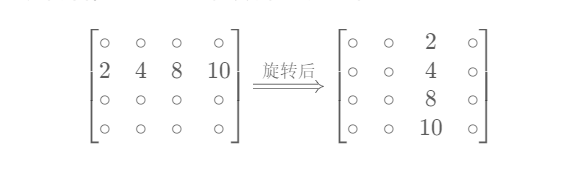
第三行、第四行依次类推,因此我们可以得出结论:
$在第 i 行 第j个元素,经过旋转之后出现在倒数第 i 列第j个位置$
也就是说转换之前的列 是转换之后的行,而转换之后的列要根据转换之前的行计算
由于我们下标从0开始,转换成代码为:
$ temp[j][n-i-1] = matrix[i][j] $
代码实现
public static void rotate(int[][] matrix) {
int n = matrix.length;
// 辅助矩阵
int[][] temp = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
temp[j][n-i-1] = matrix[i][j];
}
}
// 复制会原矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j]= temp[i][j];
}
}
}
第二种方法:原地修改
第二种方法不使用额外的矩阵,直接在原矩阵中修改。
以矩阵的四个顶点为例,它的旋转路径为:$A <—— D<—— C<—— B<—— A$ ,但是通过下图我们也可以看见,在第一步中,A的值被D的值覆盖了,因此需要使用一个额外变量 temp 保存 A的值 , 即 $A <—— D<—— C<—— B<—— temp$
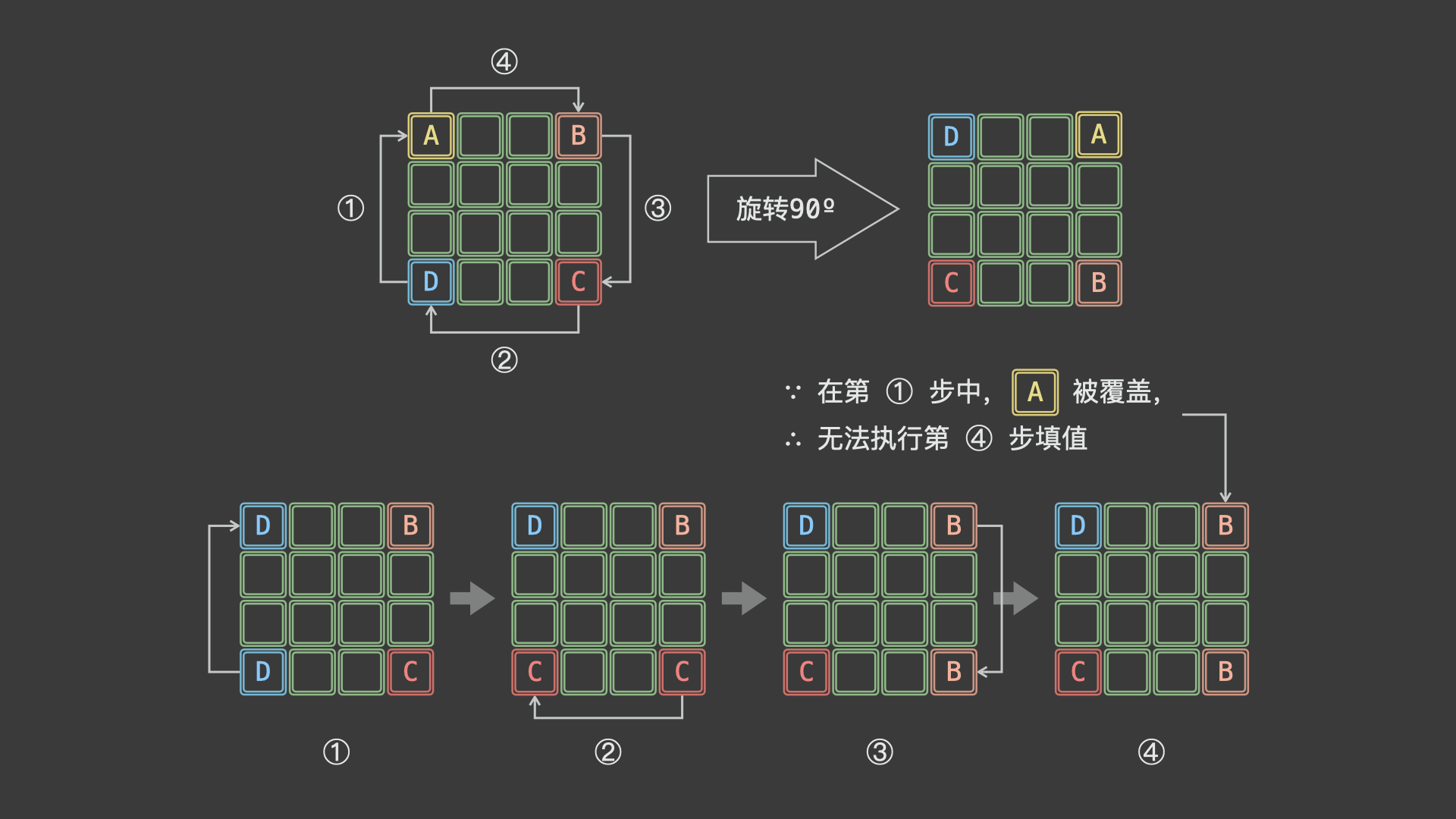
如上图所示,一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/4 的各元素为起始点执行以上旋转操作,即可完整实现矩阵旋转。
当矩阵大小 n 为偶数时,取前 n/2作为行, n/2 列的元素作为起点
当矩阵大小 n 为奇数时,取前 n/2作为行, (n+1)/2列作为元素的起点
假设起点元素matrix[i][j], 由第一种方法得出的公式,可任意推导出下面任一公式: $$ 暂存: temp = matrix[i][j] $$ $$matrix[i][j] <—— matrix[n-1-j][i] <—— matrix[j][n-i-1] <—— matrix[n-j-1][n-i-1] <—— temp$$
公式推导过程
由方法一得到关键公式为: $ temp[j][n-i-1] = matrix[i][j] $ ,这是使用辅助矩阵,如果我们想要原地修改即: $$ matrix[j][n-i-1] = matrix[i][j] $$ 但是此时我们发现,$matrix[j][n-i-1]$ 原来的值会被 $ matrix[i$][j] 覆盖掉,因此我们可以使用临时变量 temp 存储:
$$ \left{ \begin{matrix} temp = matrix[j][n-i-1] \ matrix[j][n-i-1] = matrix[i][j] \end{matrix} \right. $$ 上面的公式表示 $matrix[i][j]$ 旋转后的位置是 $ matrix[j][n-i-1]$,那么 $ matrix[j][n-i-1]$ 旋转之后的位置是什么呢?
接着将 i、j 带入关键公式,但此时的 i 和 j 变为: $$ \left{ \begin{matrix} i = j \ j = n-i-1 \end{matrix} \right. $$ 带入之后得 $ matrix[n-i-1][n-j-1]$ ,该位置就是 $matrix[j][n-i-1]$ 旋转之后所在的位置,但是仍然存在被覆盖的问题,继续使用 temp 即可,因此得出: $$ \left{ \begin{matrix} temp = matrix[n-i-1][n-j-1] \ matrix[n-i-1][n-j-1] = matrix[j][n-i-1] \ matrix[j][n-i-1] = matrix[i][j] \end{matrix} \right. $$ 紧接着继续带入 i 和 j 到关键公式: $$ \left{ \begin{matrix} i = n-i-1 \ j = n-j-1 \end{matrix} \right. $$ 带入之后得$ matrix[n-j-1][i] $ , 该位置就是 $matrix[n-i-1][n-j-1]$ 旋转之后所在的位置,继续使用 temp 保存被覆盖的值,因此有: $$ \left{ \begin{matrix} temp = [n-j-1][i] \ matrix[n-j-1][i] = matrix[n-i-1][n-j-1] \ matrix[n-i-1][n-j-1] = matrix[j][n-i-1] \ matrix[j][n-i-1] = matrix[i][j] \end{matrix} \right. $$ 紧接着继续带入 i 和 j 到关键公式: $$ \left{ \begin{matrix} i = n-j-1\ j = i \end{matrix} \right. $$ 带入之后得$ matrix[i][j]$ , 该位置就是 $matrix[n-j-1][i]$ 旋转之后所在的位置 ,继续使用 temp 保存被覆盖的值 ,因此有: $$ \left{ \begin{matrix} temp = matrix[i][j] \ matrix[i][j] = matrix[n-j-1][i] \ matrix[n-j-1][i] = matrix[n-i-1][n-j-1] \ matrix[n-i-1][n-j-1] = matrix[j][n-i-1] \ matrix[j][n-i-1] = matrix[i][j] \end{matrix} \right. $$ 到这,我们发现又回到了起点,这几个公式为一个循环,每一个旋转之后的位置就是下一个要旋转的位置,因此我们可以使用临时变量保存: $$ \left{ \begin{matrix} temp = matrix[i][j] \ matrix[i][j] = matrix[n-j-1][i] \ matrix[n-j-1][i] = matrix[n-i-1][n-j-1] \ matrix[n-i-1][n-j-1] = matrix[j][n-i-1] \ matrix[j][n-i-1] = temp \end{matrix} \right. $$
代码实现
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1) / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = tmp;
}
}
}
}
面试题 01.08. 零矩阵
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
示例 1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
示例 2:
输入:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
输出:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
思路分析
题目要求将为0元素所在的列和行都置为0,设计到查找某个元素首先肯定要遍历。找到为0的元素的位置,然后记录它所在的行和列。
知道了哪行和哪列要置为0,通过第二次遍历修改原矩阵的值。
代码实现
public static void setZeroes(int[][] matrix) {
// 行和列的长度
int rowLength = matrix.length;
int colLength = matrix[0].length;
// 使用俩个标记数组,记录0元素的行和列
boolean[] row = new boolean[rowLength];
boolean[] col = new boolean[colLength];
// 第一次遍历找到所有0元素的行和列
for (int i = 0; i < rowLength; i++) {
for (int j = 0; j < colLength; j++) {
// 记录元素为0的位置
if (matrix[i][j] == 0) row[i] = col[j] = true;
}
}
// 第二次遍历,将0元素的行和列的所有元素都置0
for (int i = 0; i < row.length; i++) {
for (int j = 0; j < col.length; j++) {
if (row[i] || col[j]) matrix[i][j] = 0;
}
}
}
498. 对角线遍历
给你一个大小为 m x n 的矩阵 mat ,请以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。
示例 1:
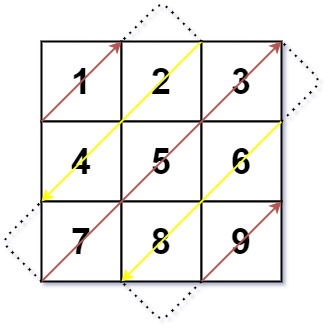
输入:mat = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,4,7,5,3,6,8,9]
示例 2:
输入:mat = [[1,2],[3,4]]
输出:[1,2,3,4]
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104-105 <= mat[i][j] <= 105
思路分析
遇到此类问题,需要找到其中的规律,既然我们要遍历对角线上的元素,我们就需要知道共有几条对角线,其次遍历对角线。
假设对角线用 i 表示,那么就有: $ i <= m+n-1$ , 若 i 从 0 开始则:$ i ∈ [0, m+n-2]$
知道了对角线的数量,我们就要找到每条对角线的规律:
规律一:
其实在例题中,我们也可以发现,颜色相同的对角线它的走向都是一样的, 红色都是从 下——》上,黄色从 上——》下,
进而我们可以总结出来:
i 为偶数: 元素遍历的顺序由 下 ——> 上
i 为奇数: 元素遍历的元素由 上 ——> 下
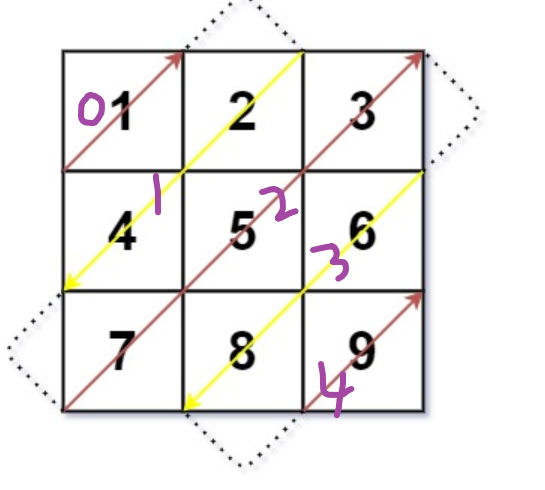
规律二:
当 元素从下往上遍历时(i为偶数),其实也可以发现 他的行是逐渐递减的,列是逐渐递加的
例如:
遍历第二条对角线的元素: mat[2][0]、 mat[1][1]、 mat[0][2]
行的变化:2——> 1 ——> 0
列的变化: 0 ——> 1 ——> 2
当 元素从上往下遍历时,其实也可以发现 他的行是逐渐递加的,列是逐渐递减的
例如:
遍历第一条对角线的元素: mat[0][1]、 mat[1][0]
行的变化:0 ——> 1
列的变化: 1 ——> 0
规律三:
知道了对角线的规律、每个元素的行和列的变化规律,我们还需要知道每条对角线的起点元素的位置。
当 元素从下往上遍历时(i为偶数),分为俩种情况:
- 当 i < m,对角线元素的起点位置为:$(i,0)$
- 当 i >= m, 对角线元素的起点位置为:$(m-1, i-m+1)$
当元素从上往下遍历时 (i为奇数),分为俩种情况:
- 当 i < n,对角线元素的起点位置为:$(0,i)$
- 当 i >= n, 对角线元素的起点位置为:$( i-n+1,n-1)$
当我第一次看到这里时,其实是很懵B的,有俩个疑问:
- 1、为什么要和m比?为什么要和n比?
- 2、起点位置又是怎么来的?
问题说明:
当元素从下往上遍历时(i为偶数),通过下图可以看出,
- 对角线以上,起点元素的行坐标是和 i 相等的,而它的列坐标不变,一直是0,因此当 i < m,起点元素的坐标为 $(i,0)$
- 对角线以下,无论有几条,起点元素的行坐标一直是 m-1 ,也就是最后一行,而它的列坐标相较于前一条对角线 的起点元素 递增加一, i - m + 1。 因此当 i >= m,起点元素的坐标为 $( i-n+1,n-1)$
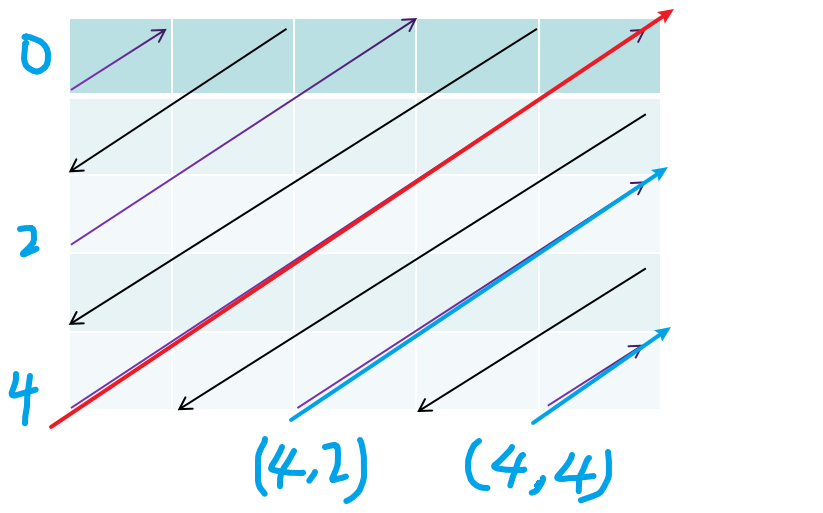
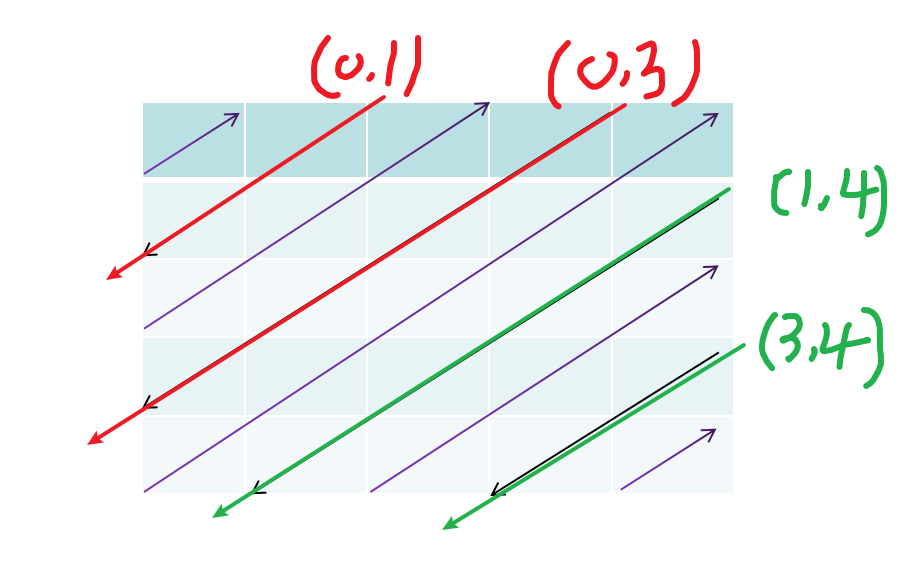
当元素从上往下遍历时(i为奇数),通过下图可以看出, 逻辑和上面的一样:
- 对角线以上,行坐标一直是0,列坐标等于 i ,因此起点元素的位置为:$(0,i)$
- 对角线以下,列坐标一直都是最后一列,即 n-1 ,行坐标 = 前一条对角线起点元素行坐标 + 1 ,即 i-n+1,因此最终位置为 $( i-n+1,n-1)$
代码实现
class Solution {
public int[] findDiagonalOrder(int[][] mat) {
int m = mat.length;
int n = mat[0].length;
int[] res = new int[m * n];
int index = 0;
// 遍历对角线
for (int i = 0; i < m + n - 1; i++) {
if (i % 2 == 1) {
// i是奇数,从上到下
int x = i < n ? 0 : i - n + 1;
int y = i < n ? i : n - 1;
while (x < m && y >= 0) {
res[index++] = mat[x][y];
x++;
y--;
}
} else {
// i是偶数,从下到上
int x = i < m ? i : m - 1;
int y = i < m ? 0 : i - m + 1;
while(y < n && x >=0){
res[index++] = mat[x][y];
x--;
y++;
}
}
}
return res;
}
}
485. 最大连续 1 的个数
给定一个二进制数组 nums , 计算其中最大连续 1 的个数。
示例 1:
输入:nums = [1,1,0,1,1,1]
输出:3
解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
示例 2:
输入:nums = [1,0,1,1,0,1]
输出:2
提示:
1 <= nums.length <= 105nums[i]不是0就是1.
思路分析
遍历 $nums$ 数组,使用 $count$ 变量累加连续1的个数, $res$ 保存最大的连续1的个数。
遇到不为1的元素停止,对 $count、res$ 去最大值,否则一直累加 $count$
在遍历完 $nums$ , 需要在对$count、res$ 去最大值,防止连续的1在数组的末尾
代码实现
public static int findMaxConsecutiveOnes(int[] nums) {
// 保存结果
int res = 0;
// 保存连续的1的个数
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 1) {
count++;
} else {
// 如果不相等,计算1的个数
// 同时将1清0,继续计算下一个连续的1的个数
res = Math.max(count, res);
count = 0;
}
}
// 这里在进行比较是为了: 数组中连续的1在数组的末尾
res = Math.max(count, res);
return res;
}
118. 杨辉三角
给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
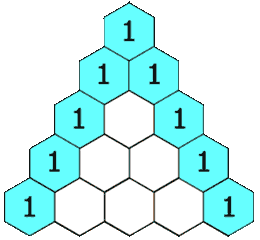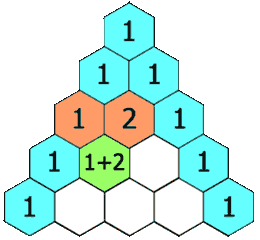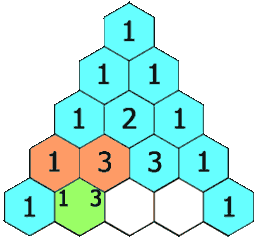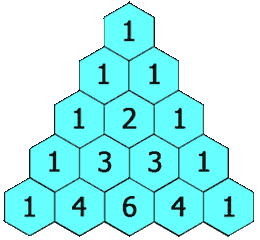
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
1 <= numRows <= 30
思路分析
杨辉三角性质:
- 行数与元素个数相等,即:第n行有n个元素
- 每一行的首元素和尾元素都是1
- 除开首尾元素,每一个元素的和都是它左上方元素和右上方元素的和
代码实现
public static List<List<Integer>> generate(int numRows) {
ArrayList<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < numRows; i++) {
// 每一行
ArrayList<Integer> row = new ArrayList<>();
// j表示每一行的元素
for (int j = 0; j <= i; j++) {
// 每行的第一个元素,与最后一个元素都是1
if (j == 0 || j == i) {
row.add(1);
}else {
// 除了首尾元素,每一个元素都是左上方与右上方的和
row.add(res.get(i-1).get(j-1) + res.get(i-1).get(j));
}
}
res.add(row);
}
return res;
}
26. 删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按 非严格递增 排列
思路分析
题意很简单,就是删除数组中 重复的元素,并保持相对顺序。
什么是相对顺序?比如 2、3, 2在3前面,删除后不能2跑到3后面去。
众所周知,数组中无法删除元素,所以采用的是快慢指针覆盖的方法
- 使用 l、r快慢指针
- l 指向重复的元素,r指向替换 l 的元素
- 当 $nums[l] != nums[r] $, 将 r 指向的元素覆盖 l+1指向的元素。即:$nums[l+1] = nums[r]$
- 当 $nums[l] == nums[r] $, 只需要移动 r 指针
为什么要覆盖 l+1 呢?
这是因为题目中要求保持相对顺序,l 指针指向的是重复元素的第一个,因此 nums[l+1] = nums[l]
(1)如下图所示,l 作为慢指针,r作为快指针,因此循环条件应该是: r<nums.length
(2) 当 l 和 r 指向的元素相等时,l 指针就停止,r继续移动,直到找到 l 与 r 不相等时,将 r 指向的元素覆盖 l + 1指向的元素
需要注意的是,每次覆盖完,l指针是+1的,所以在执行完,此时的 l 指针应该为4 ,最终返回有效数组的长度为:l+1
代码实现
class Solution {
public int removeDuplicates(int[] nums) {
int l = 0;
int r = 1;
while(r < nums.length) {
// 如果不相等, 则覆盖 l+1处的重复元素
if (nums[l] != nums[r]) {
nums[l+1] = nums[r];
// 覆盖完,将l指针右移
l++;
}
r++;
}
return l+1;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104-231 <= nums[i] <= 231 - 1
**进阶:**你能尽量减少完成的操作次数吗?
思路分析
思路和26题一样,仍然使用快慢指针。
l指针指向元素0,r指针指向不为0的元素,将其交换即可。
代码实现
需要注意的是,left和right指针都是从0开始
public void moveZeroes(int[] nums) {
if(nums == null || nums.length == 1) return;
// 定义双指针
int left = 0, right = 0;
while (right < nums.length) {
if (nums[right] != 0) {
// 交换
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
left++;
}
right++;
}
}
